Die Welt der Simulation: Ein Blick in die Finite-Elemente-Methode (FEM)

Die Finite-Elemente-Methode (FEM), auch als Finite-Elemente-Analyse (FEA) bekannt, ist ein numerisches Verfahren zur Lösung von physikalischen Problemen, das in verschiedenen Ingenieurdisziplinen und in der Physik weit verbreitet ist. Die Methode basiert auf der Diskretisierung eines Berechnungsgebiets, also der Unterteilung in eine endliche Anzahl kleinerer, einfacherer Teile, die als finite Elemente bezeichnet werden. Diese Elemente sind in der Regel geometrische Formen wie Tetraeder, Hexaeder oder Quader.

Funktionsweise der FEM

Die FEM-Analyse erfolgt in der Regel in vier Schritten:

• 1. Preprocessing (Modellvorbereitung): Zunächst wird das zu analysierende Modell in einem CAD-Programm erstellt und in eine FEM-Software eingelesen. Das Modell wird dann in finite Elemente unterteilt, ein Prozess, der als Meshing bezeichnet wird. Die Feinheit der Unterteilung beeinflusst die Genauigkeit der Ergebnisse, erhöht aber auch die Rechenzeit.
• 2. Definition der Parameter: Nachdem das Netz vorbereitet ist, werden Materialien, ihr Verhalten und äußere Belastungen definiert. Auch Randbedingungen, wie mögliche Belastungen, werden festgelegt.
• 3. Berechnung: Die FEM-Software berechnet die Gleichungen, die sich aus den festgelegten Parametern ergeben. Dabei werden die physikalischen Gesetze auf die finiten Elemente angewandt, um das Verhalten des Gesamtmodells unter verschiedenen Bedingungen zu simulieren.
• 4. Postprocessing (Ergebnisauswertung): Im letzten Schritt werden die Ergebnisse der Berechnung ausgewertet. Dies umfasst die grafische Darstellung der Ergebnisgrößen, wie Spannungen, Verschiebungen und Dehnungen, und kann auch Farbplots umfassen, die einen schnellen Überblick über die Ergebnisse ermöglichen.

Parameter einer FEM-Analyse

Bei einer FEM-Analyse sind verschiedene Parameter von entscheidender Bedeutung, um genaue und zuverlässige Ergebnisse zu erzielen. Diese Parameter umfassen:

• Materialdefinition und -verhalten:
  Die Eigenschaften des Materials, einschließlich Elastizitätsmodul, Poisson-Zahl, Dichte und gegebenenfalls plastisches Verhalten, müssen definiert werden. Diese Materialparameter beeinflussen, wie das Modell auf Belastungen reagiert.
• Äußere Belastungen:
  Die Art und Weise, wie Lasten und Kräfte auf das Modell aufgebracht werden, ist entscheidend. Dies umfasst die Größe, Richtung und Verteilung der Lasten sowie dynamische Effekte und Stoßbelastungen.
• Randbedingungen:
  Die Randbedingungen definieren, wie das Modell im Raum fixiert ist und welche Bewegungen oder Verformungen an bestimmten Stellen zugelassen oder verhindert werden. Sie sind entscheidend für die realistische Simulation des Verhaltens des Modells unter Last.
• Kontaktbedingungen:
  In vielen Fällen interagieren verschiedene Teile eines Modells miteinander, was durch Kontaktbedingungen beschrieben wird. Diese definieren, wie Oberflächen aufeinander reagieren, zum Beispiel durch Reibung oder Bindung.
• Netzfeinheit und Elementqualität:
  Die Netzfeinheit und die Qualität der verwendeten Elemente sind wichtig für die Genauigkeit der Spannungsverläufe und die Vermeidung von Singularitäten oder übermäßigen Verformungen der Elemente.
• Last-Zeit-Verlauf:
  Bei dynamischen Analysen ist der Verlauf der Last über die Zeit hinweg wichtig, um das Verhalten des Modells unter variierenden Belastungen zu verstehen.
• Festhaltungen:
  Wie und wo das Bauteil im Modell festgehalten wird, beeinflusst die Ergebnisse der Simulation. Die Festhaltungen müssen die tatsächlichen Einspannbedingungen im realen Einsatz widerspiegeln.

Diese Parameter müssen sorgfältig ausgewählt und definiert werden, um eine realistische Simulation des Verhaltens des Modells unter den vorgesehenen Betriebsbedingungen zu gewährleisten. Die Genauigkeit der FEM-Analyse hängt stark von der korrekten Definition dieser Parameter ab.

Anwendungsbereiche

Die FEM wird in einer Vielzahl von Bereichen eingesetzt, darunter Maschinenbau, Bauwesen, Automobil-, Luft- und Raumfahrttechnik sowie in der Elektroindustrie und Optik. Sie ermöglicht es, komplexe Konstruktionen und physikalische Phänomene zu analysieren und Vorhersagen über ihre Verhaltensweise unter realen Bedingungen zu treffen.

Die Finite-Elemente-Methode (FEM) wird in der Praxis in einer Vielzahl von Branchen und Anwendungsbereichen eingesetzt, um komplexe Strukturen und Systeme zu analysieren und zu optimieren. Hier sind einige konkrete Beispiele für den Einsatz der FEM in der Praxis:

• Maschinenbau und Fahrzeugtechnik:
  In diesen Bereichen wird die FEM genutzt, um die Festigkeit und Steifigkeit von Bauteilen zu analysieren. Dies ist besonders wichtig für die Entwicklung von Komponenten, die hohen Belastungen standhalten müssen, wie zum Beispiel in der Automobil- oder Luftfahrtindustrie.
• Bauingenieurwesen:
  Hier wird die FEM verwendet, um die strukturelle Integrität von Bauwerken wie Brücken, Hochhäusern und Staudämmen zu bewerten. Sie hilft dabei, die Reaktion von Strukturen auf Lasten wie Wind, Erdbeben und Schnee zu simulieren.
• Elektrotechnik und Optik:
  In diesen Feldern kann die FEM zur Simulation elektromagnetischer Felder und zur Optimierung optischer Systeme eingesetzt werden.
• Medizintechnik:
  Die FEM findet Anwendung in der Analyse von biomechanischen Systemen, wie zum Beispiel bei der Untersuchung von Knochenstrukturen oder der Optimierung von Implantaten.
• Materialwissenschaft und Werkstofftechnik:
  Die FEM ermöglicht es, das Verhalten von Materialien unter verschiedenen Belastungen und Umgebungsbedingungen zu untersuchen und zu optimieren.
• Additive Fertigung (3D-Druck):
  Die FEM wird genutzt, um die Festigkeit und Stabilität von 3D-gedruckten Bauteilen zu berechnen, die oft in ihrer Topologie optimiert werden, um Material und Gewicht einzusparen.
• Produktentwicklung:
  In der Produktentwicklung wird die FEM eingesetzt, um mechanische Festigkeitsberechnungen durchzuführen, aufwändige Tests zu reduzieren und die Anzahl physischer Prototypen zu minimieren.
• Ausbildung und Forschung:
  Die FEM wird auch in der akademischen Welt für Lehrzwecke und Forschung verwendet, um Studierenden und Forschenden ein tieferes Verständnis für die komplexen Zusammenhänge in verschiedenen physikalischen Systemen zu vermitteln.
• Softwareentwicklung:
  Es gibt eine Vielzahl von FEM-Softwarelösungen, die von verschiedenen Anbietern entwickelt und vertrieben werden. Diese reichen von kommerziellen Produkten bis hin zu Open-Source- oder Freeware-Optionen, die insbesondere für kleinere Unternehmen oder Einsteiger interessant sein können.

In der Praxis ist es wichtig, dass die FEM korrekt angewendet wird, um zuverlässige Ergebnisse zu erzielen. Dies erfordert eine sorgfältige Modellierung, die richtige Wahl der Materialparameter und Randbedingungen sowie eine fundierte Interpretation der Ergebnisse durch erfahrene Ingenieure und Fachleute.

Softwareempfehlungen für FEM-Analysen

Verschiedene Software-Hersteller bieten Lösungen für Finite-Elemente-Berechnungen (FEM) an. Diese reichen von umfassenden Simulationsplattformen bis hin zu spezialisierten Anwendungen für bestimmte Branchen oder Anwendungsfälle. Es gibt aber auch eine kostenlose Open-Source Option, um FEM-Analysen durchzuführen.

FreeCad ist eine kostenlose und quelloffene Software für computergestütztes Design (CAD), die auf allen gängigen Plattformen wie Windows, Linux und macOS läuft. Sie bietet umfangreiche Funktionen für die 3D-Modellierung, Baugruppenkonstruktion und Erstellung technischer Zeichnungen. Dank der Möglichkeit, die Software durch Python-Skripte und Drittanbieter-Workbenches zu erweitern, ist FreeCad äußerst flexibel und anpassbar.

Eine besonders leistungsstarke Komponente von FreeCad ist das Modul für Finite-Elemente-Berechnungen (FEM). Dieses ermöglicht es, Strukturanalysen an 3D-Modellen durchzuführen und Verformungen, Spannungen sowie Verschiebungen unter Belastung zu simulieren. Der Workflow reicht von der Geometrieerstellung über die Vernetzung bis hin zur Lösung und Visualisierung der Ergebnisse. Dabei kann FreeCad auf externe Solver wie CalculiX und Netgen für die Vernetzung und Berechnung zurückgreifen, es besteht aber auch die Möglichkeit, eigene Solver wie fcFEM zu integrieren.

Die benutzerfreundliche grafische Oberfläche des FEM-Moduls erleichtert das Aufbringen von Randbedingungen und die Zuweisung von Materialien erheblich. Insgesamt macht diese leistungsfähige Komponente FreeCad zu einer attraktiven Open-Source-Lösung für Finite-Elemente-Analysen im Bereich der Strukturmechanik.

Was hat eine FEM Analyse mit Werkstoffkunde zu tun?

Eine FEM-Analyse hat eine enge Verbindung zur Werkstoffkunde, da die Eigenschaften der verwendeten Materialien eine zentrale Rolle in der Simulation und Analyse von Strukturen und Bauteilen spielen. Die Werkstoffkunde befasst sich mit der Untersuchung und Charakterisierung von Materialien, um deren Verhalten unter verschiedenen Bedingungen zu verstehen. Dieses Wissen ist für die FEM-Analyse aus folgenden Gründen wichtig:

• Materialparameter:
  Für eine realistische FEM-Simulation müssen die Materialparameter wie Elastizitätsmodul, Poisson-Zahl, Dichte, Fließgrenze und Härte bekannt sein. Diese Parameter beschreiben, wie ein Material auf äußere Belastungen reagiert, und sind entscheidend für die Genauigkeit der FEM-Ergebnisse.
• Materialverhalten:
  Die Werkstoffkunde liefert Informationen über das Verhalten von Materialien unter Last, einschließlich elastischer, plastischer und viskoelastischer Eigenschaften. Die FEM muss dieses Verhalten modellieren können, um beispielsweise bleibende Verformungen oder das Ermüdungsverhalten von Materialien vorherzusagen.
• Anisotropie:
  Viele Materialien, insbesondere Verbundwerkstoffe, weisen anisotrope Eigenschaften auf, was bedeutet, dass ihre mechanischen Eigenschaften richtungsabhängig sind. Die Werkstoffkunde hilft dabei, diese Eigenschaften zu charakterisieren, die dann in der FEM-Analyse berücksichtigt werden müssen.
• Werkstoffversagen:
  Die Vorhersage von Werkstoffversagen, wie Bruch oder Rissbildung, ist ein wichtiger Aspekt der FEM-Analyse. Die Werkstoffkunde liefert die Grundlagen für Versagenskriterien und -modelle, die in der FEM verwendet werden, um die Sicherheit und Zuverlässigkeit von Konstruktionen zu bewerten.
• Wärmebehandlung und thermische Eigenschaften:
  Die Werkstoffkunde untersucht auch das Verhalten von Materialien unter thermischen Belastungen und nach Wärmebehandlungen. Diese Informationen sind für FEM-Analysen relevant, die thermische Effekte oder temperaturabhängige Materialveränderungen berücksichtigen.
• Mikrostruktur:
  Die Mikrostruktur eines Materials beeinflusst seine makroskopischen Eigenschaften. Die Werkstoffkunde ermöglicht ein Verständnis der Mikrostruktur, das für fortgeschrittene FEM-Analysen genutzt werden kann, um das Materialverhalten auf mikroskopischer Ebene zu simulieren.

Insgesamt ist die Werkstoffkunde grundlegend für die korrekte Anwendung der FEM-Analyse, da sie die erforderlichen Daten und das Verständnis für das Materialverhalten liefert, das für die Modellierung und Simulation von realen physikalischen Systemen erforderlich ist.

Herausforderungen von FEM-Analysen

In der FEM-Analyse gibt es verschiedene Herausforderungen und ungelöste Probleme, die sowohl die mathematische Modellierung als auch die praktische Anwendung betreffen. Einige dieser Probleme umfassen:

• 1. Höhere Fehlerordnung bei speziellen Elementen: Die Erwartung einer höheren Fehlerordnung bei der Verwendung spezieller Elemente in der FEM-Analyse hängt stark von der zusätzlichen Glattheit der Lösung der gegebenen Randwertaufgabe ab. Dies bedeutet, dass die Genauigkeit der Ergebnisse nicht immer wie erwartet verbessert wird, es sei denn, die Lösung erfüllt bestimmte Glattheitskriterien.
• 2. Erweiterungen der FEM für spezifische Probleme: Es gibt verschiedene Erweiterungen der FEM, wie gemischte finite Elemente, nichtkonforme finite Elemente und die diskontinuierliche Galerkin-Methode, die für spezifische Probleme entwickelt wurden. Diese Erweiterungen adressieren Herausforderungen wie Nebenbedingungen in Gleichungen oder die Anwendung auf Probleme höherer Ordnung. Jedoch erfordern sie spezifisches Wissen und Erfahrung in der Anwendung und können in der Praxis komplex in der Umsetzung sein.
• 3. Nichtlineare Probleme: Viele reale Probleme sind nichtlinear, was bedeutet, dass Annahmen wie die Linearitätsannahme (eine Verdopplung der Last führt zu einer Verdopplung der Durchbiegung und Spannung) nicht zutreffen. Die Modellierung und Lösung nichtlinearer Probleme stellt eine erhebliche Herausforderung dar, da sie oft komplexe mathematische und numerische Techniken erfordern.
• 4. Fehlerquellen und Ungenauigkeiten: Die FEM ist ein mathematisches Näherungsverfahren, und eine gewisse Fehlertoleranz ist bereits durch den Lösungsalgorithmus vorgegeben. Neben diesen mathematisch bedingten Ungenauigkeiten gibt es Fehlerquellen, die aus mangelndem problemspezifischem Fachwissen oder softwarespezifischen Einschränkungen resultieren können. Die Auswahl der geeigneten Software und die korrekte Anwendung der Methode sind entscheidend, um diese Fehlerquellen zu minimieren.
• 5. Probleme bei der Anwendung auf dynamische Prozesse: Die Simulation dynamischer Prozesse verfügt über ausgeprägtere Fehlerquellen im Vergleich zu statischen Simulationen. Der Versuch, Bauteilsymmetrien auszunutzen, die in statischen Fällen zu effizienteren Berechnungen führen, kann bei dynamischen Simulationen zu falschen Ergebnissen führen.

Diese ungelösten Probleme und Herausforderungen erfordern kontinuierliche Forschung und Entwicklung in der FEM, um die Methoden und Techniken weiter zu verbessern und an die komplexen Anforderungen realer Anwendungen anzupassen.

Materialverhalten unter Belastung

Die Fehlertheorie befasst sich mit der Vorhersage und Analyse von Materialversagen unter verschiedenen Belastungsbedingungen. Sie ist ein wesentlicher Bestandteil der Werkstoffwissenschaft und der mechanischen Konstruktionsprinzipien, da sie hilft zu bestimmen, unter welchen Bedingungen ein Material oder eine Struktur versagen könnte. Zwei zentrale Konzepte in der Fehlertheorie, die häufig in der Finite-Elemente-Methode (FEM) Anwendung finden, sind die Tresca- und von Mises-Vergleichsspannungskriterien. Diese Kriterien werden verwendet, um das Versagen von duktilen Materialien unter mehrachsigen Spannungszuständen zu bewerten.

Tresca-Kriterium

Das Tresca-Kriterium, auch als Schubspannungstheorie bekannt, basiert auf der maximalen Scherspannung in einem Material. Es postuliert, dass Versagen eintritt, wenn die maximale Scherspannung in einem Material einen kritischen Wert erreicht, der durch die Scherfestigkeit des Materials bei einachsiger Belastung bestimmt wird. Mathematisch wird das Tresca-Kriterium durch die größte Differenz zwischen den Hauptspannungen ausgedrückt:

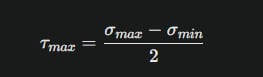
wobei $$\sigma_{max}$$ und $$\sigma_{min}$$ die maximale und minimale Hauptspannung sind. Das Tresca-Kriterium ist besonders nützlich für die Analyse von Materialien, die unter hohen Scherspannungen versagen, und wird oft in der Metallverarbeitung und bei der Bewertung von Schweißnähten verwendet.

Von Mises-Kriterium

Das von Mises-Kriterium, auch als Gestaltänderungsenergiehypothese bekannt, basiert auf der Annahme, dass Versagen auftritt, wenn die von Mises-Vergleichsspannung einen kritischen Wert erreicht, der der Fließgrenze des Materials unter einachsiger Belastung entspricht. Dieses Kriterium berücksichtigt den gesamten Spannungszustand und ist für die Vorhersage des Beginns des plastischen Fließens unter mehrachsigen Belastungen geeignet. Die von Mises-Vergleichsspannung wird wie folgt berechnet:

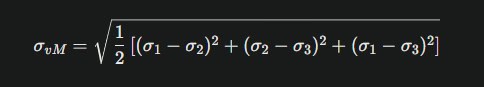
wobei $$\sigma_1$$, $$\sigma_2$$, und $$\sigma_3$$ die Hauptspannungen sind. Das von Mises-Kriterium wird häufig in der FEM-Analyse verwendet, um das Verhalten von duktilen Materialien unter komplexen Belastungsbedingungen zu bewerten.

Anwendung in der FEM-Analyse

In der FEM-Analyse werden das Tresca- und von Mises-Kriterium verwendet, um kritische Bereiche in einer Struktur zu identifizieren, in denen das Risiko eines Materialversagens besteht. Durch die Berechnung der Vergleichsspannungen können Ingenieure entscheiden, ob ein Material oder eine Konstruktion unter den gegebenen Belastungen sicher ist oder ob Änderungen am Design oder Material erforderlich sind, um ein Versagen zu verhindern. Diese Kriterien tragen dazu bei, die Sicherheit und Zuverlässigkeit von Konstruktionen in verschiedenen Anwendungsbereichen zu gewährleisten.

Vorteile von FEM-Analysen

Die Vorteile der FEM liegen in ihrer Fähigkeit, komplexe Probleme zu lösen, die mit klassischen analytischen Methoden nicht oder nur schwer lösbar sind. Sie ermöglicht eine detaillierte Analyse von Strukturen und kann dabei helfen, die Entwicklung von Prototypen und die Durchführung von physischen Tests zu reduzieren.

Allerdings müssen bei der FEM-Analyse die Randbedingungen korrekt definiert werden, da sonst die Ergebnisse nicht zuverlässig sind. Zudem erfordert die Methode eine sorgfältige Vorbereitung des Modells und eine genaue Definition der Materialparameter und Belastungen. Software übernimmt zwar viele Berechnungen automatisch, jedoch sind manuelle Anpassungen an kritischen Stellen und die Interpretation der Ergebnisse durch erfahrene Ingenieure notwendig.